TEORIA GRACELI COMPOSTA QUÂNTICA DE CAMPOS - ELETROD. ELETTROFRAC E DIMENSIONAL GRACELI

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

Eletrodinâmica quântica (EDQ), ou QED, de Quantum electrodynamics, é uma teoria quântica de campos do eletromagnetismo. A EDQ descreve todos os fenômenos envolvendo partículas eletricamente carregadas interagindo por meio da força eletromagnética. Sua capacidade de predição de grandezas como o momento magnético anômalo do múon e o desvio de Lamb dos níveis de energia do hidrogênio a tornou uma teoria renomada.

História

A eletrodinâmica foi a evolução natural das teorias da antigamente denominada segunda quantização, isto é, quantização dos campos, ao ramo da eletrodinâmica.

As teorias de campo são necessariamente relativísticas, já que admitindo-se que haja partículas mensageiras na troca de energia e momento mediados pelo campo, essas mesmas partículas, a exemplo do fóton (que historicamente precedeu a descoberta das teorias de quantização do campo) devem se deslocar a velocidades próximas ou igual à da luz no vácuo (c = 299 792 458 m/s).

A primeira formulação da eletrodinâmica quântica é atribuída a Paul Dirac, que nos anos 1920 foi capaz de calcular o coeficiente de emissão espontânea do átomo.^[1] Essa teoria se desenvolveu a partir dos trabalhos Sin-Itiro Tomonaga, Julian Schwinger e Richard Feynman. Pelos seus trabalhos, eles ganharam o prêmio Nobel de Física em 1965.

Desenvolvimento formal

A eletrodinâmica quântica é uma teoria abeliana de calibre, dotada de um grupo de calibre U(1).

O campo de calibre que media a interação entre campos de spin 1/2, é o campo eletromagnético, que se apresenta sob a forma de fótons.

A descrição da interação se dá através da lagrangiana para a interação entre elétrons e pósitrons, que é dada por:

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

{\mathcal {L}}=\psi ^{*}(i\gamma ^{\mu }D_{\mu }-m)\psi -{\frac {1}{4}}F_{\mu \nu }F^{\mu \nu }

onde $\ \psi$ e sua adjunta de Dirac $\psi ^{*}$ são os campos representando partículas eletricamente carregadas, especificamente, os campos do elétron e pósitron representados como espinores de Dirac.

Na física de partículas, a interação eletrofraca ou força eletrofraca é a descrição unificada de duas das quatro interações fundamentais conhecidas da natureza: o eletromagnetismo e a interação fraca. Embora essas duas forças pareçam muito diferentes nas baixas energias diárias, a teoria as modela como dois aspectos diferentes da mesma força. Acima da energia de unificação, da ordem de 246 GeV, elas se fundiriam em uma única força. Assim, se o universo estiver quente o suficiente (aproximadamente 1015 K, uma temperatura não ultrapassada desde logo após o Big Bang), então a força eletromagnética e a força fraca se fundirão em uma força eletrofraca combinada. Durante a Era Quark, a força eletrofraca se dividia em força eletromagnética e fraca.

Sheldon Glashow, Abdus Salam,^[1]^[2] e Steven Weinberg^[3] foram agraciados com o Prêmio Nobel de Física de 1979 por suas contribuições para a unificação da interação fraca e eletromagnética entre partículas elementares, conhecida como teoria de Weinberg-Salam.^[4]^[5] A existência de interações eletrofracas foi experimentalmente estabelecida em dois estágios, o primeiro sendo a descoberta de correntes neutras no espalhamento de neutrinos pela colaboração de Gargamelle em 1973, e o segundo em 1983 pelas colaborações UA1 e UA2 que envolveram a descoberta dos bósons de calibre W e Z em colisões próton-antipróton no acelerador Super Proton Synchrotron. Em 1999, Gerardus 't Hooft e Martinus Veltman receberam o prêmio Nobel por mostrar que a teoria eletrofraca é renormalizável.

História

Depois que o experimento de Wu descobriu a violação de paridade na interação fraca, uma busca começou por uma maneira de relacionar as interações fraca e eletromagnética. Estendendo o trabalho de seu orientador de doutorado Julian Schwinger, Sheldon Glashow primeiro experimentou introduzir duas simetrias diferentes, uma quiral e uma aquiral, e combinou-as de forma que sua simetria geral permanecesse ininterrupta. Isso não gerou uma teoria renormalizável e a simetria teve que ser quebrada à mão, pois nenhum mecanismo espontâneo era conhecido, mas previu uma nova partícula, o bóson Z. Isso recebeu pouca atenção, pois não correspondeu a nenhum achado experimental.

Em 1964, Salam e Weinberg tiveram a mesma ideia, mas previram um fóton sem massa e três bósons de calibre massivos com uma simetria quebrada manualmente. Mais tarde, por volta de 1967, ao investigar a quebra espontânea de simetria, Weinberg encontrou um conjunto de simetrias que previa um bóson de calibre neutro sem massa. Inicialmente rejeitando tal partícula como inútil, mais tarde ele percebeu que suas simetrias produziram a força eletrofraca, e ele passou a prever massas aproximadas para W e Z bósons . Significativamente, ele sugeriu que essa nova teoria era renormalizável.^[3] Em 1971, Gerard 't Hooft provou que simetrias de calibre quebradas espontaneamente são renormalizáveis mesmo com bósons de calibre massivos.

Formulação

O ângulo de mistura eletrofraca de Weinberg θ

\theta _{W}

e a relação entre as constantes de acoplamento g, g′ e e . Adaptado do livro de TD Lee, Particle Physics and Introduction to Field Theory (1981)

A distribuição de isospin fraco,

T_{3}

, e hipercarga fraca,

Y_{W}

, das partículas elementares conhecidas, mostrando a carga elétrica, Q , ao longo do ângulo de mistura eletrofraca. O campo neutro de Higgs (no círculo) quebra a simetria eletrofraca e interage com outras partículas para dar-lhes massa. Três componentes do campo de Higgs tornam-se parte dos massivos bósons W e Z

Matematicamente, o eletromagnetismo é unificado com as interações fracas como um campo de Yang-Mills com um grupo de calibre SU(2) × U(1) , que descreve as operações formais que podem ser aplicadas aos campos de calibre eletrofracos sem alterar a dinâmica do sistema. Estes domínios são os campos de isospin fraco W₁, W₂, e W₃, e o campo de hipercarga fraca B. Essa invariância é conhecida como simetria eletrofraca.

Os geradores de SU(2) e U(1) recebem o nome de isospin fraco (chamado de T) e hipercarga fraca (chamada de Y), respectivamente. Estes então dão origem aos bósons de calibre que medeiam as interações eletrofracas - os três bósons W de isospin fraco W₁, W₂, e W₃ e o bóson B de hipercarga fraca, respectivamente, todos os quais são "inicialmente" sem massa. Esses ainda não são campos físicos, antes da quebra espontânea da simetria e do mecanismo de Higgs associado.

No modelo padrão, os bósons W^± e Z⁰ e o fóton são produzidos por meio da quebra espontânea de simetria eletrofraca SU(2) × U(1)_Y a U(1)_em, efetuada pelo mecanismo de Higgs (ver também bóson de Higgs), um elaborado fenômeno teórico de campo quântico que "espontaneamente" altera a realização da simetria e reorganiza os graus de liberdade.^[6]^[7]^[8]^[9]

A carga elétrica surge como uma combinação linear (não trivial) de Y (hipercarga fraca) e o componente T₃ do isospin fraco ( $Q=T_{3}+{\tfrac {1}{2}}Y_{\mathrm {W} }$ ) que não se acopla ao bóson de Higgs - ou seja, o Higgs e o campo eletromagnético não têm efeito um sobre o outro no nível das forças fundamentais ("nível de árvore"), enquanto qualquer outra combinação linear da hipercarga e do isospin fraco irá interagir com o Higgs. Isso causa uma separação aparente entre a força fraca, que interage com o Higgs, e o eletromagnetismo, que não interage. Matematicamente, a carga elétrica é uma combinação específica da hipercarga e T₃ delineada na figura.

U(1)_em (o grupo de simetria do eletromagnetismo) é definido como o grupo gerado por esta combinação linear especial, e a simetria descrita por este grupo é ininterrupta, uma vez que não interage diretamente com o Higgs (mas o faz por meio de flutuações quânticas).

A quebra espontânea de simetria acima faz com que os bósons W₃ e B se aglutinem em dois bósons físicos diferentes com massas diferentes - o bóson Z₀ e o fóton (γ),

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

{\mathcal {L}}=\psi ^{*}(i\gamma ^{\mu }D_{\mu }-m)\psi -{\frac {1}{4}}F_{\mu \nu }F^{\mu \nu }

//////

{\begin{pmatrix}\gamma \\Z^{0}\end{pmatrix}}={\begin{pmatrix}\cos \theta _{\text{W}}&\sin \theta _{\text{W}}\\-\sin \theta _{\text{W}}&\cos \theta _{\text{W}}\end{pmatrix}}{\begin{pmatrix}B\\W_{3}\end{pmatrix}},

onde $θ W$ é o ângulo de mistura eletrofraca. Os eixos que representam as partículas, essencialmente apenas foram rodados no plano (W₃, B) pelo ângulo $θ W$ . Isso também introduz uma incompatibilidade entre as massas das partículas
Z0
e
W±
(denotadas como $M Z$ e $M W$ , respectivamente),

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

{\mathcal {L}}=\psi ^{*}(i\gamma ^{\mu }D_{\mu }-m)\psi -{\frac {1}{4}}F_{\mu \nu }F^{\mu \nu }

//////

M_{\text{Z}}={\frac {M_{\text{W}}}{\cos \theta _{\text{W}}}}.

Os bósons $W 1$ e $W 2$ , por sua vez, combinam-se para produzir bósons massivos carregados

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

{\mathcal {L}}=\psi ^{*}(i\gamma ^{\mu }D_{\mu }-m)\psi -{\frac {1}{4}}F_{\mu \nu }F^{\mu \nu }

//////

W^{\pm }={\frac {1}{\sqrt {2}}}(W_{1}\mp iW_{2}).

Lagrangiano

Antes da quebra de simetria eletrofraca

O Lagrangiano para as interações eletrofracas é dividido em quatro partes antes que a quebra de simetria eletrofraca se manifeste,

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

{\mathcal {L}}=\psi ^{*}(i\gamma ^{\mu }D_{\mu }-m)\psi -{\frac {1}{4}}F_{\mu \nu }F^{\mu \nu }

//////

{\mathcal {L}}_{\text{EW}}={\mathcal {L}}_{g}+{\mathcal {L}}_{f}+{\mathcal {L}}_{h}+{\mathcal {L}}_{y}~.

O termo ${\mathcal {L}}_{g}$ descreve a interação entre os três bósons vetoriais W e o bóson vetorial B,

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

{\mathcal {L}}=\psi ^{*}(i\gamma ^{\mu }D_{\mu }-m)\psi -{\frac {1}{4}}F_{\mu \nu }F^{\mu \nu }

//////

{\mathcal {L}}_{g}=-{\tfrac {1}{4}}W_{a}^{\mu \nu }W_{\mu \nu }^{a}-{\tfrac {1}{4}}B^{\mu \nu }B_{\mu \nu }

onde $W^{a\mu \nu }$ ( $a=1,2,3$ ) e $B^{\mu \nu }$ são os tensores de intensidade de campo para os campos de calibre de isospin fraco e hipercarga fraca.

${\mathcal {L}}_{f}$ é o termo cinético para o Modelo Padrão de férmions. A interação entre os bósons de calibre e os férmions se dão pela derivade covariante de calibre,

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

{\mathcal {L}}=\psi ^{*}(i\gamma ^{\mu }D_{\mu }-m)\psi -{\frac {1}{4}}F_{\mu \nu }F^{\mu \nu }

//////

{\mathcal {L}}_{f}={\overline {Q}}_{i}iD\!\!\!\!/\;Q_{i}+{\overline {u}}_{i}iD\!\!\!\!/\;u_{i}+{\overline {d}}_{i}iD\!\!\!\!/\;d_{i}+{\overline {L}}_{i}iD\!\!\!\!/\;L_{i}+{\overline {e}}_{i}iD\!\!\!\!/\;e_{i}

onde o subscrito i percorre as três gerações de férmions; Q, u e d são os campos de quarks correspondendo ao dubleto levógiro, singleto dextrógiro up, e singleto dextrógiro down; e L e e são os campos de elétrons do dubleto levógiro e singleto dextrógiro. A barra de Feynman $D\!\!\!\!/$ significa a contração do quadri-gradiente com as matrizes de Dirac

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

{\mathcal {L}}=\psi ^{*}(i\gamma ^{\mu }D_{\mu }-m)\psi -{\frac {1}{4}}F_{\mu \nu }F^{\mu \nu }

//////

D\!\!\!\!/=\gamma ^{\mu }D_{\mu }

e a derivada covariante é (excluindo o campo de calibre do glúon para a interação forte)

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

{\mathcal {L}}=\psi ^{*}(i\gamma ^{\mu }D_{\mu }-m)\psi -{\frac {1}{4}}F_{\mu \nu }F^{\mu \nu }

//////

D_{\mu }:=\partial _{\mu }-i{\frac {g'}{2}}Y\,B_{\mu }-i{\frac {g}{2}}T_{j}\,W_{\mu }^{j}

Aqui $�$ é a hipercarga fracais e $T_{j}$ são os componentes do isospin fraco.

O termo ${\mathcal {L}}_{h}$ descreve o campo de Higgs e suas interações consigo mesmo e com os bósons de calibre,

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

{\mathcal {L}}=\psi ^{*}(i\gamma ^{\mu }D_{\mu }-m)\psi -{\frac {1}{4}}F_{\mu \nu }F^{\mu \nu }

//////

{\mathcal {L}}_{h}=|D_{\mu }h|^{2}-\lambda \left(|h|^{2}-{\frac {v^{2}}{2}}\right)^{2}

O termo ${\mathcal {L}}_{y}$ descreve a interação de Yukawa com os férmions,

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

{\mathcal {L}}=\psi ^{*}(i\gamma ^{\mu }D_{\mu }-m)\psi -{\frac {1}{4}}F_{\mu \nu }F^{\mu \nu }

//////

{\mathcal {L}}_{y}=-y_{u\,ij}\epsilon ^{ab}\,h_{b}^{\dagger }\,{\overline {Q}}_{ia}u_{j}^{c}-y_{d\,ij}\,h\,{\overline {Q}}_{i}d_{j}^{c}-y_{e\,ij}\,h\,{\overline {L}}_{i}e_{j}^{c}+h.c.~,

e gera suas massas, manifestas quando o campo de Higgs adquire um valor esperado do vácuo diferente de zero, discutido a seguir.

Depois da quebra de simetria eletrofraca

O Lagrangiano se reorganiza à medida que o bóson de Higgs adquire um valor esperado do vácuo diferente do zero, ditado pelo potencial da seção anterior. Como resultado dessa reescrita, a quebra de simetria se torna manifesta. Na história do universo, acredita-se que isso tenha acontecido logo após o big bang quente, quando o universo estava a uma temperatura de 159,5±1,5 GeV^[10] (assumindo o Modelo Padrão da física de partículas).

Devido à sua complexidade, este Lagrangiano é melhor descrito dividindo-o em várias partes como segue.

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

{\mathcal {L}}=\psi ^{*}(i\gamma ^{\mu }D_{\mu }-m)\psi -{\frac {1}{4}}F_{\mu \nu }F^{\mu \nu }

//////

{\mathcal {L}}_{\text{EW}}={\mathcal {L}}_{\text{K}}+{\mathcal {L}}_{\text{N}}+{\mathcal {L}}_{\text{C}}+{\mathcal {L}}_{\text{H}}+{\mathcal {L}}_{\text{HV}}+{\mathcal {L}}_{\text{WWV}}+{\mathcal {L}}_{\text{WWVV}}+{\mathcal {L}}_{\text{Y}}.

O termo cinético ${\mathcal {L}}_{K}$ contém todos os termos quadráticos da Lagrangiana, que incluem os termos dinâmicos (as derivadas parciais) e os termos de massa (visivelmente ausentes da Lagrangiana antes da

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

{\mathcal {L}}=\psi ^{*}(i\gamma ^{\mu }D_{\mu }-m)\psi -{\frac {1}{4}}F_{\mu \nu }F^{\mu \nu }

////// quebra de simetria)

{\begin{aligned}{\mathcal {L}}_{\text{K}}=\sum _{f}{\overline {f}}(i\partial \!\!\!/\!\;-m_{f})f-{\frac {1}{4}}A_{\mu \nu }A^{\mu \nu }-{\frac {1}{2}}W_{\mu \nu }^{+}W^{-\mu \nu }+m_{W}^{2}W_{\mu }^{+}W^{-\mu }\\\qquad -{\frac {1}{4}}Z_{\mu \nu }Z^{\mu \nu }+{\frac {1}{2}}m_{Z}^{2}Z_{\mu }Z^{\mu }+{\frac {1}{2}}(\partial ^{\mu }H)(\partial _{\mu }H)-{\frac {1}{2}}m_{H}^{2}H^{2}~,\end{aligned}}

onde a soma percorre todos os férmions da teoria (quarks e léptons), e os campos $A_{\mu \nu }$ , $Z_{\mu \nu }$ , $W_{\mu \nu }^{-}$ , and $W_{\mu \nu }^{+}\equiv (W_{\mu \nu }^{-})^{\dagger }$ são dados como

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

{\mathcal {L}}=\psi ^{*}(i\gamma ^{\mu }D_{\mu }-m)\psi -{\frac {1}{4}}F_{\mu \nu }F^{\mu \nu }

//////

X_{\mu \nu }^{a}=\partial _{\mu }X_{\nu }^{a}-\partial _{\nu }X_{\mu }^{a}+gf^{abc}X_{\mu }^{b}X_{\nu }^{c}~,

com ‘ $�$ ’ a ser substituído pelo campo relevante ( $�$ , $�$ , $W^{\pm }$ ), e $f abc$ pelas constantes de estrutura do grupo de calibres apropriado.

As componentes do Lagrangiano para a corrente neutra ${\mathcal {L}}_{\text{N}}$ e para a corrente carregada ${\mathcal {L}}_{\text{C}}$ contêm as interações entre os férmions e os bósons de calibre,

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

{\mathcal {L}}=\psi ^{*}(i\gamma ^{\mu }D_{\mu }-m)\psi -{\frac {1}{4}}F_{\mu \nu }F^{\mu \nu }

//////

{\mathcal {L}}_{\text{N}}=eJ_{\mu }^{\text{em}}A^{\mu }+{\frac {g}{\cos \theta _{W}}}(J_{\mu }^{3}-\sin ^{2}\theta _{W}J_{\mu }^{\text{em}})Z^{\mu }\,,

onde $e=g\sin \theta _{\text{W}}=g'\cos \theta _{\text{W}}\,.$ A corrente eletromagnética $J_{\mu }^{\text{em}}$ é

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

{\mathcal {L}}=\psi ^{*}(i\gamma ^{\mu }D_{\mu }-m)\psi -{\frac {1}{4}}F_{\mu \nu }F^{\mu \nu }

//////

J_{\mu }^{\text{em}}=\sum _{f}q_{f}{\overline {f}}\gamma _{\mu }f

onde $q_{f}^{}$ são as cargas elétricas dos férmions. A corrente neutra fraca $J_{\mu }^{3}$ é

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

{\mathcal {L}}=\psi ^{*}(i\gamma ^{\mu }D_{\mu }-m)\psi -{\frac {1}{4}}F_{\mu \nu }F^{\mu \nu }

//////

J_{\mu }^{3}=\sum _{f}I_{f}^{3}{\overline {f}}\gamma _{\mu }{\frac {1-\gamma ^{5}}{2}}f

onde $I_{f}^{3}$ é o isospin fraco dos férmions.

A parte da corrente carregada da Lagrangiana é dada por

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

{\mathcal {L}}=\psi ^{*}(i\gamma ^{\mu }D_{\mu }-m)\psi -{\frac {1}{4}}F_{\mu \nu }F^{\mu \nu }

//////

{\mathcal {L}}_{\text{C}}=-{\frac {g}{\sqrt {2}}}\left[{\overline {u}}_{i}\gamma ^{\mu }{\frac {1-\gamma ^{5}}{2}}M_{ij}^{\text{CKM}}d_{j}+{\overline {\nu }}_{i}\gamma ^{\mu }{\frac {1-\gamma ^{5}}{2}}e_{i}\right]W_{\mu }^{+}+{\text{h.c.}}~,

onde ${\mathcal {L}}_{\text{H}}$ contém os termos de auto interação de três e quatro pontos de Higgs,

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

{\mathcal {L}}=\psi ^{*}(i\gamma ^{\mu }D_{\mu }-m)\psi -{\frac {1}{4}}F_{\mu \nu }F^{\mu \nu }

//////

{\mathcal {L}}_{\text{H}}=-{\frac {gm_{H}^{2}}{4m_{W}}}H^{3}-{\frac {g^{2}m_{H}^{2}}{32m_{W}^{2}}}H^{4}~.

${\mathcal {L}}_{\text{HV}}$ contém as interações de Higgs com os bósons vetoriais de calibre,

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

{\mathcal {L}}=\psi ^{*}(i\gamma ^{\mu }D_{\mu }-m)\psi -{\frac {1}{4}}F_{\mu \nu }F^{\mu \nu }

//////

{\mathcal {L}}_{\text{HV}}=\left(gm_{W}H+{\frac {g^{2}}{4}}H^{2}\right)\left(W_{\mu }^{+}W^{-\mu }+{\frac {1}{2\cos ^{2}\theta _{W}}}Z_{\mu }Z^{\mu }\right).

${\mathcal {L}}_{\text{WWV}}$ contém as auto interações de três pontos de calibre,

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

{\mathcal {L}}=\psi ^{*}(i\gamma ^{\mu }D_{\mu }-m)\psi -{\frac {1}{4}}F_{\mu \nu }F^{\mu \nu }

//////

{\mathcal {L}}_{\text{WWV}}=-ig[(W_{\mu \nu }^{+}W^{-\mu }-W^{+\mu }W_{\mu \nu }^{-})(A^{\nu }\sin \theta _{W}-Z^{\nu }\cos \theta _{W})+W_{\nu }^{-}W_{\mu }^{+}(A^{\mu \nu }\sin \theta _{W}-Z^{\mu \nu }\cos \theta _{W})].

${\mathcal {L}}_{\text{WWVV}}$ contém as auto interações de quatro pontos de calibre,

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

{\mathcal {L}}=\psi ^{*}(i\gamma ^{\mu }D_{\mu }-m)\psi -{\frac {1}{4}}F_{\mu \nu }F^{\mu \nu }

//////

{\begin{aligned}{\mathcal {L}}_{\text{WWVV}}=-{\frac {g^{2}}{4}}{\Big \{}&[2W_{\mu }^{+}W^{-\mu }+(A_{\mu }\sin \theta _{W}-Z_{\mu }\cos \theta _{W})^{2}]^{2}\\&-[W_{\mu }^{+}W_{\nu }^{-}+W_{\nu }^{+}W_{\mu }^{-}+(A_{\mu }\sin \theta _{W}-Z_{\mu }\cos \theta _{W})(A_{\nu }\sin \theta _{W}-Z_{\nu }\cos \theta _{W})]^{2}{\Big \}}.\end{aligned}}

${\mathcal {L}}_{\text{Y}}$ contém as interações Yukawa entre os férmions e o campo de Higgs,

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

{\mathcal {L}}=\psi ^{*}(i\gamma ^{\mu }D_{\mu }-m)\psi -{\frac {1}{4}}F_{\mu \nu }F^{\mu \nu }

//////

{\mathcal {L}}_{\text{Y}}=-\sum _{f}{\frac {gm_{f}}{2m_{W}}}{\overline {f}}fH.

Note os fatores ${\tfrac {1}{2}}(1-\gamma ^{5})$ nos acoplamentos fracos: esses fatores projetam os componentes levógiros dos campos de spinor. É por isso que se diz que a teoria eletrofraca é uma teoria quiral.

Em física nuclear e física de partículas, a interação fraca, que também é chamada de força fraca ou força nuclear fraca, é uma das 4 interações fundamentais conhecidas, sendo as outras a interação eletromagnética, a interação forte e a gravitação. Ela é o mecanismo de interação entre partículas subatômicas que é responsável pelo decaimento radioativo de átomos: A interação fraca participa da fissão nuclear e da fusão nuclear. A teoria que descreve seu comportamento e efeitos é às vezes chamada de dinâmica quântica de sabor (QFD, do inglês quantum flavourdynamics), entretanto, o termo QFD é raramente usado, já que a força fraca é melhor compreendida pela teoria eletrofraca (EWT, do inglês electroweak theory).^[1]

O alcance efetivo da força fraca está limitado às distâncias subatômicas, e é menor do que o diâmetro de um próton.^[2]

Contexto

O Modelo Padrão de física de partículas provê uma estrutura uniforme para o entendimento das interações eletromagnética, fraca e forte. Uma interação ocorre quando duas partículas (geralmente, mas não necessariamente, férmions com spin semi-inteiro) trocam bósons portadores de força com spin inteiro. Os férmions envolvidos em tais trocas podem ser elementares (e.g. elétrons ou quarks) ou compostos (e.g. prótons ou nêutrons), apesar de que nos níveis mais fundamentais, todas as interações fracas ocorrem entre partículas elementares.

Na interação fraca, férmions podem trocar três tipos de portadores de força, a saber os bósons $W$ , $W$ , e $Z$ . As massas desses bósons são muito maiores do que a massa de um próton ou um nêutron, o que é consistente com o alcance curto da força fraca. Na verdade, a força é denominada fraca porque sua intensidade de campo para qualquer dada distância é tipicamente várias ordens de grandeza menor do que a da força eletromagnética, que por sua vez é várias ordens de grandeza menor do que a força nuclear forte.

A interação fraca é a única interação fundamental que quebra a simetria de paridade, e similarmente, mas muito mais raramente, a única interação a quebrar a simetria de carga-paridade.

Quarks, que compõem partículas compostas como nêutrons e prótons, vêm em seis “sabores” – up, down, estranho, charmoso, top e bottom – que dão às partículas compostas suas propriedades. A interação fraca é a única que permite aos quarks trocarem seus sabores. A troca dessas propriedades é mediada pelos bósons portadores de força. Por exemplo, durante um decaimento beta menos, um quark down dentro de um nêutron é alterado para um quark up, convertendo o nêutron em um próton e resultando na emissão de um elétron e um antineutrino do elétron. Outro exemplo importante de fenômeno envolvendo a interação fraca é a fusão do hidrogênio em hélio que alimenta o processo termonuclear do Sol.

A maioria dos férmions decai por uma interação fraca ao longo do tempo. Tais decaimentos tornam possível a datação por radiocarbono, já que o carbono-14 decai para o nitrogênio-14 através da força fraca. Ela também pode criar radioluminescência, comumente usada na luminescência de trítio, e no campo relacionado de betavoltaicos^[3] (mas a não similar luminescência de rádio).

A força eletrofraca foi separada nas forças eletromagnética e fraca durante a era quark do universo primitivo.

História

Em 1933, Enrico Fermi propôs a primeira teoria da interação fraca, conhecida como interação de Fermi. Ele sugeriu que o decaimento beta poderia ser explicado por uma interação de quatro férmions, envolvendo uma força de contato sem alcance.^[4]^[5] Assim numa interação fraca um neutrino é sempre produzido com um pósitron, ou um antineutrino com um elétron, o que dá um conjunto de carga eletricamente carregado.

Entretanto, ela é melhor descrita como um campo de força sem contato de alcance finito, embora muito curto.^[^{carece de fontes]} Na década de 1960, Sheldon Glashow, Abdus Salam e Steven Weinberg unificaram a força eletromagnética e a interação fraca ao mostrar que eram dois aspectos de uma única força, agora denominada a força eletrofraca.^[6]^[7]

A Gargamela no museu Microcosmo do CERN.

Em 1973, a equipe que realizou experiências na câmara de bolhas Gargamela com um feixe de neutrinos do CERN apresentou a primeira evidência direta da existência de interação fraca eletricamente neutra, a força nuclear fraca.^[8]

A existência dos bósons W e Z não havia sido confirmada diretamente até 1983.^[9]

Propriedades

Um diagrama representando as rotas de decaimento devido à interação fraca carregada e alguns indicadores de suas probabilidades. A intensidade das linhas é dada pelos parâmetros CKM.

A interação fraca eletricamente carregada é única em vários aspectos:

É a única interação que pode mudar o sabor de quarks e léptons (i.e., alterar o tipo de um quark para outro).
É a única interação que viola a simetria de paridade. É também a única que viola a simetria carga-paridade.
Ambas as interações eletricamente carregada e eletricamente neutra são mediadas (propagadas) por partículas portadoras de força que possuem massas expressivas, uma propriedade incomum que é explicada no Modelo Padrão pelo mecanismo de Higgs.

Devido às suas grandes massas (aproximadamente 90 GeV/c²^[10]) essas partículas portadoras, chamadas de bósons W e Z, têm vida curta com um tempo de vida abaixo de 10⁻²⁴ segundos.^[11] A interação fraca possui uma constante de acoplamento (um indicador de quão frequentemente as interações ocorrem) entre 10⁻⁷ e 10⁻⁶, em comparação à constante de acoplamento eletromagnética que está em torno de 10⁻² e à constante de acoplamento da interação forte que está em torno de $1$ ;^[12] consequentemente a interação fraca é ‘fraca’ em termos de intensidade.^[13] A interação fraca possui um alcance efetivo muito pequeno (em torno de 10⁻¹⁷ à 10⁻¹⁶ m (0.01 a 0.1 fm)).^[a]^[14]^[15] A distâncias em torno de 10⁻¹⁸ metros (0.001 fm), a interação fraca possui intensidade de magnitude similar a da força eletromagnética, mas que começa a diminuir exponencialmente com o aumento da distância. Ampliada por apenas uma ordem e meia de grandeza de magnitude, a distâncias em torno de 3×10⁻¹⁷ m, a interação fraca se torna 10,000 vezes mais fraca.^[16]

A interação fraca afeta todos os férmions do Modelo Padrão, assim como o bóson de Higgs; neutrinos interagem somente pela gravidade e pela interação fraca. A interação fraca não produz estados ligados nem envolve energias de ligação – algo que a gravidade faz em escala astronômica, que a força eletromagnética faz a níveis moleculares e atômicos, e a força nuclear forte faz somente a nível subatômico, dentro do núcleo.^[17]

Seu efeito mais notável é devido à sua primeira característica única: a interação fraca carregada produz mudança de sabor. Por exemplo, um nêutron é mais pesado que um próton (seu nucleon associado), e pode decair em um próton pela troca do sabor (tipo) de um de seus dois quarks down para um quark up. Nem a interação forte nem o eletromagnetismo permitem a troca de sabor, logo isso só pode ocorrer pelo decaimento fraco; sem o decaimento fraco, certas propriedades dos quarks como a estranheza e o charme (associadas com o quark estranho e o quark charmoso, respectivamente) também teriam que ser conservadas através de todas as interações.

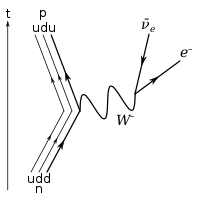
Todos os mésons são instáveis devido ao decaimento fraco.^[18]^: No processo conhecido por decaimento beta, um quark down em um nêutron pode mudar para um quark up ao emitir um bóson $W -$ virtual que então decai em um elétron e um antineutrino do elétron.^[19]^: Outro exemplo é a captura eletrônica – uma variante comum do decaimento radioativo – onde um próton e um elétron dentro de um átomo interagem, e mudam para um nêutron (um quark up muda para um quark down) e um neutrino do elétron é emitido.

Devido às grandes massas dos bósons W, as transformações de partículas ou decaimentos (e.g., mudança de sabor) que dependem da interação fraca ocorrem tipicamente muito mais devagar do que transformações ou decaimentos que dependem somente das forças forte ou eletromagnética. Por exemplo, um píon neutro decai eletromagneticamente, e portanto tem uma vida de somente 10⁻¹⁶ segundos. Diferentemente, um píon carregado só pode decair pela força fraca, e portanto existe por volta de 10⁻⁸ segundos, ou cem milhões de vezes mais tempo do que um píon neutro.^[20] Um exe mplo particularmente extremo é o decaimento por força fraca de um nêutron livre, que leva em torno de 15 minutos.^[21]^:

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

{\mathcal {L}}=\psi ^{*}(i\gamma ^{\mu }D_{\mu }-m)\psi -{\frac {1}{4}}F_{\mu \nu }F^{\mu \nu }

//////

Isospin fraco e hipercarga fraca

Férmions levógiros no Modelo Padrão^[22]
1ª Geração			2ª Geração			3ª Geração
Férmion	Símbolo	Isospin Fraco	Férmion	Símbolo	Isospin Fraco	Férmion	Símbolo	Isospin Fraco
Neutrino do elétron	$ν e$	$+{\tfrac {1}{2}}$	Neutrino do múon	$ν μ$	$+{\tfrac {1}{2}}$	Neutrino do tau	$ν τ$	$+{\tfrac {1}{2}}$
Elétron	$e -$	$-{\tfrac {1}{2}}$	Múon	$μ -$	$-{\tfrac {1}{2}}$	Tau	$τ -$	$-{\tfrac {1}{2}}$
Quark up	u	$+{\tfrac {1}{2}}$	Quark charmoso	$c$	$+{\tfrac {1}{2}}$	Quark top	$t$	$+{\tfrac {1}{2}}$
Quark Down	d	$-{\tfrac {1}{2}}$	Quark estranho	$s$	$-{\tfrac {1}{2}}$	Quark bottom	$b$	$-{\tfrac {1}{2}}$
Todas as partículas levógiras (regulares) acima possuem anti-partículas dextrógiras correspondentes com isospin igual e oposto.
Todas as partículas dextrógiras (regulares) e antipartículas levógiras possuem isospin fraco igual a 0.

Todas as partículas têm a propriedade chamada de isospin fraco (símbolo T₃), que serve como um número quântico aditivo que restringe como a partícula interage com os $W \pm$ da força fraca. O isospin fraco desempenha o mesmo papel na interação fraca com $W \pm$ que a carga elétrica desempenha no eletromagnetismo, e a carga de cor na interação forte; um número diferente com um nome similar, carga fraca, discutida abaixo, é usada para interações com o $Z$ . Todos os férmions levógiros possuem como valor de isospin fraco $+{\tfrac {1}{2}}$ ou $-{\tfrac {1}{2}}$ ; todos os férmions dextrógiros tem isospin 0. Por exemplo, o quark up tem $T_{3}=+{\tfrac {1}{2}}$ e o quark down tem $T_{3}=-{\tfrac {1}{2}}$ . Um quark nunca decai pela interação fraca em um quark com o mesmo $T_{3}$ : Quarks com um $T_{3}$ de $+{\tfrac {1}{2}}$ somente decaem em quarks com $T_{3}=-{\tfrac {1}{2}}$ e vice-versa.

Decaimento do π+ através da interação fraca

Para qualquer dada interação, o isospin fraco é conservado: A soma dos números de isospin fraco de partículas entrando na interação é igual a soma dos números de isospin fraco das partículas saindo da interação. Por exemplo, um $\pi ^{+}$ (levógiro), com um isospin fraco igual a $+1$ normalmente decai em um $ν μ$ (com $T_{3}=+{\tfrac {1}{2}}$ ) e um $μ +$ (como uma antipartícula dextrógira, $+{\tfrac {1}{2}}$ ).^[23]^:

Para o desenvolvimento da teoria eletrofraca, outra propriedade, a hipercarga fraca, foi inventada, definida como:

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

{\mathcal {L}}=\psi ^{*}(i\gamma ^{\mu }D_{\mu }-m)\psi -{\frac {1}{4}}F_{\mu \nu }F^{\mu \nu }

//////

Y_{\text{W}}=2\,\left(\,Q-T_{3}\,\right)~,

onde $Y_{\text{W}}$ é a hipercarga fraca de uma partícula com carga elétrica $Q$ (em unidades de carga elementar) e isospin fraco $T_{3}$ . Hipercarga fraca é a geradora da componente U(1) do grupo de gauge eletrofraco; enquanto algumas partículas têm isospin fraco igual a zero, todas as partículas de spin ${\tfrac {1}{2}}$ conhecidas têm hipercarga fraca diferente de zero.

Tipos de interações

Existem dois tipos de interação fraca (chamados de vértices). O primeiro tipo é chamado de “interação de corrente-carregada” porque os férmions fracamente interagentes formam uma corrente com carga elétrica total não nula. O segundo tipo é chamado de “interação de corrente-neutra” porque os férmions fracamente interagentes formam uma corrente com carga elétrica total nula. Ela é responsável pela (rara) deflexão de neutrinos. Os dois tipos de interação seguem diferentes regras de seleção. Essa convenção de nomenclatura é muitas vezes mal interpretada para rotular a carga elétrica do bósons W e Z, entretanto a convenção de nomenclatura antecede o conceito de bósons mediadores, e claramente (pelo menos no nome) rotula a carga da corrente (formada pelos férmions), não necessariamente os bóson.[f]

Interação de corrente-carregada

O diagrama de Feynman para o decaimento beta-menos de um nêutron em um próton, elétron e um antineutrino do elétron, por intermédio de bóson W- pesado

Em um tipo de interação de corrente carregada, um lépton carregado (tal como um elétron ou um múon, tendo carga -1) podem absorver um bóson W+ (uma partícula de carga +1) e ser deste modo convertida em neutrino correspondente (com carga 0), onde o tipo (“sabor”) do neutrino (elétron, múon ou tau) é o mesmo do tipo de lépton na interação, por exemplo:

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

{\mathcal {L}}=\psi ^{*}(i\gamma ^{\mu }D_{\mu }-m)\psi -{\frac {1}{4}}F_{\mu \nu }F^{\mu \nu }

//////

\mu ^{-}+W^{+}\to \nu _{\mu }

Similarmente, um quark down (d com carga -⅓) pode ser convertido em um quark up (u com carga +⅔) ao emitir um bóson W⁻ ou ao absorver um bóson W⁺. Mais precisamente o quark down se torna uma superposição quântica de quarks up: isso que dizer ele possui a possibilidade de se tornar qualquer um dos 3 tipos de quark up, com as probabilidades dadas pelas tabelas da matriz CKM. Por outro lado, um quark up pode emitir um bóson W⁺, ou absorver um bóson W⁻, e deste modo ser convertido em um quark down, por exemplo:

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

{\mathcal {L}}=\psi ^{*}(i\gamma ^{\mu }D_{\mu }-m)\psi -{\frac {1}{4}}F_{\mu \nu }F^{\mu \nu }

//////

{\begin{aligned}d&\to u+W^{-}\\d+W^{+}&\to u\\c&\to s+W^{+}\\c+W^{-}&\to s\end{aligned}}

O bóson W é instável e portanto decairá rapidamente, com um tempo de vida muito curto. Por exemplo:

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

{\mathcal {L}}=\psi ^{*}(i\gamma ^{\mu }D_{\mu }-m)\psi -{\frac {1}{4}}F_{\mu \nu }F^{\mu \nu }

//////

{\begin{aligned}W^{-}&\to e^{-}+{\bar {\nu }}_{e}~\\W^{+}&\to e^{+}+\nu _{e}~\end{aligned}}

Pode ocorrer o decaimento de um bóson W em outros produtos, com diversas probabilidades.^[24]

No assim chamado decaimento beta de um nêutron (veja a imagem acima), um quark down dentro do nêutron emite um bóson ${\text{W}}^{-}$ virtual e é deste modo convertido em um quark up, convertendo o nêutron em um próton. Por causa da energia limitada envolvida no processo (i.e., a diferença de massa entre o quark down e o quark up), o bóson virtual W⁻ pode carregar somente energia suficiente para produzir um elétron e um antineutrino do elétron – as duas menores massas possíveis entre os futuros produtos de decaimento.^[25] Ao nível dos quarks, o processo pode ser representado como:

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

{\mathcal {L}}=\psi ^{*}(i\gamma ^{\mu }D_{\mu }-m)\psi -{\frac {1}{4}}F_{\mu \nu }F^{\mu \nu }

//////

d\to u+e^{-}+{\bar {\nu }}_{e}~

Interação de corrente-neutra

Em interações de corrente neutra, um quark ou um lépton (e.g., um elétron ou um múon) emite ou absorve um bóson ${\text{Z}}$ neutro. Por exemplo:

e^{-}\to e^{-}+Z^{0}

Assim como os bósons ${\text{W}}^{\pm }$ , o bóson ${\text{Z}}^{0}$ também decai rapidamente,^[26] por exemplo:

Z^{0}\to b+{\bar {b}}

Diferente da interação de corrente-carregada, cujas regras de seleção são rigidamente limitadas pela quiralidade, carga elétrica, e / ou isospin fraco, a interação de corrente-neutra por ${\text{Z}}^{0}$ pode causar a deflexão entre dois férmions quaisquer do modelo padrão: Tanto partículas ou antipartículas, com qualquer carga elétrica, e ambas as quiralidades levógiras e dextrógiras, embora a intensidade da interação difere.

O número quântico da carga fraca ( $Q_{\text{W}}$ ) serve o mesmo propósito na interação de corrente neutra com o ${\text{Z}}^{0}$ que a carga elétrica ( $�$ , sem subscrito) faz na interação eletromagnética: Ele quantifica a parte vetorial da interação. Seu valor é dado por:^[27]

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

{\mathcal {L}}=\psi ^{*}(i\gamma ^{\mu }D_{\mu }-m)\psi -{\frac {1}{4}}F_{\mu \nu }F^{\mu \nu }

//////

Q_{\text{W}}=2\,T_{3}-4\,Q\,\sin ^{2}\theta _{\text{W}}=2\,T_{3}-Q+\left(1-4\,\sin ^{2}\theta _{\text{W}}\right)\,Q~.

Já que o ângulo de mistura fraco $\theta _{\text{W}}\approx 26^{\circ }$ , a expressão entre parêntesis $\left(1-4\sin ^{2}\theta _{\text{W}}\right)\approx 0.060$ , com seu valor mudando pouco com a diferença de momento linear (chamada de “running”) entre as partículas envolvidas. Consequentemente

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

{\mathcal {L}}=\psi ^{*}(i\gamma ^{\mu }D_{\mu }-m)\psi -{\frac {1}{4}}F_{\mu \nu }F^{\mu \nu }

//////

Q_{\text{W}}\approx 2\,T_{3}-Q=\operatorname {sgn}(Q)\,\left(1-\left|Q\right|\right)~,

uma vez que por convenção $\operatorname {sgn} T_{3}\equiv \operatorname {sgn} Q$ , e para todos os férmions envolvidos na interação fraca $T_{3}=\pm {\tfrac {1}{2}}$ . A carga fraca dos léptons carregados é próxima de zero, logo eles interagem na sua maior parte com os bósons $Z$ pelo acoplamento axial.

Teoria eletrofraca

O Modelo Padrão de física de partículas descreve a interação eletromagnética e a interação fraca como dois aspectos de uma única interação eletrofraca. Essa teoria foi desenvolvida por volta de 1968 por Sheldon Glashow, Abdus Salam, e Steven Weinberg, e eles foram premiados com o Prêmio Nobel de Física de 1979 por seus trabalhos.^[28] O mecanismo de Higgs fornece uma explicação para a presença de três bóson de gauge massivos ( ${\text{W}}^{+}$ , ${\text{W}}^{-}$ , ${\text{Z}}^{0}$ , os três portadores da interação fraca), e o fóton sem massa ( $\gamma$ , o portador da interação eletromagnética).^[29]

De acordo com a teoria eletrofraca, a energias muito altas, o universo tem quatro componentes do campo de Higgs cujas interações são portadas por quatro bósons de gauge sem massa – cada um similar ao fóton – formando um dubleto escalar complexo do campo de Higgs. Da mesma forma, existem quatro bósons eletrofracos sem massa. Entretanto, a baixas energias, essa simetria de gauge é quebrada espontaneamente para a simetria ${\text{U}}(1)$ do eletromagnetismo, já que um dos campos de Higgs adquire um valor esperado de vácuo. Ingenuamente, seria esperado que a quebra de simetria produzisse três bósons sem massa, mas em vez disso esses três bósons de Higgs “extra” são incorporados nos três bósons fracos, que então adquirem massa pelo mecanismo de Higgs. Esses três bósons compostos são os bósons ${\text{W}}^{+}$ , ${\text{W}}^{+}$ e ${\text{Z}}^{0}$ realmente observados na interação fraca. O quarto bóson de gauge eletrofraco é o fóton ( $\gamma$ ) do eletromagnetismo que não se acopla a nenhum outro campo de Higgs e portanto permanece sem massa.^[30]

Essa teoria fez uma série de previsões, incluindo a previsão das massas dos bósons ${\text{Z}}$ e ${\text{W}}$ antes de suas descobertas e detecções em 1983.

No dia 4 de Julho de 2012, as equipes experimentais CMS e ATLAS no Grande Colisor de Hádrons (Large Hadron Collider) anunciaram independentemente que eles confirmaram a descoberta formal de um bóson anteriormente desconhecido de massa entre 125 e 127 GeV/ $c$ ², cujo comportamento até então era “consistente com” um bóson de Higgs, embora adicionando uma nota cautelosa que mais dados e análises eram necessários antes de identificar positivamente o novo bóson como sendo um bóson de Higgs de algum tipo. Até o dia 14 de Março de 2013, a existência de um bóson de Higgs foi provisoriamente confirmada.^[31]

Em um caso especulativo em que a escala de quebra de simetria eletrofraca fosse reduzida, a interação ininterrupta ${\text{SU}}(2)$ acabaria se tornando confinante. Modelos alternativos onde o ${\text{SU}}(2)$ se torna confinante acima dessa escala parecem quantitativamente semelhantes ao Modelo Padrão a energias mais baixas, mas dramaticamente diferentes acima da quebra de simetria.^[32]

Violação de simetria

Partículas levógiras e dextrógiras:

�

é o momento linear da partícula e

�

é o seu spin. Observe a falta de simetria reflexiva entre os estados.

As leis da natureza foram por muito tempo consideradas como invariantes sob a reflexão de um espelho. Era esperado que os resultados de um experimento visto por um espelho seriam idênticos aos resultados de uma cópia espelhada do aparato experimental, construída separadamente, vista pelo espelho. Essa lei chamada de conservação da paridade era conhecida por ser respeitada pela gravitação clássica, eletromagnetismo e a interação forte; assumia-se que era uma lei universal.^[33] Entretanto, em meados da década de 1950 Chen-Ning Yang e Tsung-Dao Lee sugeriram que a interação fraca poderia violar essa lei. Chien Shiung Wu e colaboradores descobriram em 1957 que a interação fraca viola a paridade, dando a Yang e Lee o Prêmio Nobel de Física de 1957.^[34]

Apesar da interação fraca ter sido descrita pela teoria de Fermi, a descoberta da violação de paridade e a teoria de renormalização sugeria que era necessária uma nova abordagem. Em 1957, Robert Marshak e George Sudarshan e, um pouco depois, Richard Feynman e Murray Gell-Mann propuseram uma Lagrangeana V − A (vetor menos vetor axial ou levógiro) para as interações fracas. Nessa teoria, a interação fraca atua somente nas partículas levógiras (e antipartículas dextrógiras). Já que a reflexão de uma partícula levógira é dextrógira, isso explica a violação máxima de paridade. A teoria V − A foi desenvolvida antes da descoberta do bóson Z, e assim ela não incluía os campos dextrógiros que aparecem na interação de corrente neutra.

Entretanto, essa teoria permitia a conservação da simetria combinada CP. A simetria CP combina paridade P (trocando levógiro por dextrógiro) com a conjugação de carga C (trocando partículas por antipartículas). Os físicos foram surpreendidos novamente em 1964, quando James Cronin e Val Fitch apresentaram evidências concretas de que a simetria CP poderia ser também quebrada em decaimentos de káons, dando a eles o Prêmio Nobel de Física de 1980.^[35] Em 1973, Makoto Kobayashi e Toshihide Maskawa mostraram que a violação de CP na interação fraca requer mais do que duas gerações de partículas,^[36] efetivamente prevendo a existência de uma ainda desconhecida terceira geração. Essa descoberta deu a eles metade do Prêmio Nobel de Física de 2008.^[37]

Diferentemente da violação de paridade, a violação de CP ocorre somente em raras circunstâncias. Apesar de sua ocorrência limitada sob as presentes condições, acredita-se que ela é a razão para a maior presença de matéria em relação a antimatéria no universo, e logo forma uma das três condições de Andrei Sakharov para a bariogênese.^[38]

Pesquisar este blog

TEORIA GRACELI COMPOSTA QUÂNTICA DE CAMPOS - ELETROD. ELETTROFRAC E DIMENSIONAL GRACELI

História

Desenvolvimento formal

História

Formulação

Lagrangiano

Antes da quebra de simetria eletrofraca

Depois da quebra de simetria eletrofraca

Contexto

História

Propriedades

Isospin fraco e hipercarga fraca

Tipos de interações

Interação de corrente-carregada

Interação de corrente-neutra

Teoria eletrofraca

Violação de simetria

Comentários

Postar um comentário